第16回 公差 Part4
第4章-4
第4章 公差
3. 幾何公差(その2)
3. 幾何公差のJIS定義
| 公差の種類 | 記 号 | 幾何公差のJIS定義 |
|---|---|---|
| 真直度公差 |  |
真直度とは、直線形体の幾何学的に正しい直線からの狂いの大きさをいう。 |
| 平面度公差 |  |
平面度とは、平面形体の幾何学的に正しい平面からの狂いの大きさをいう。 |
| 真円度公差 |  |
真円度とは、円形形体の幾何学的に正しい円からの狂いの大きさをいう。 |
| 円筒度公差 |  |
円筒度とは、円筒形体の幾何学的に正しい円筒からの狂いの大きさをいう。 |
| 線の輪郭度公差 |  |
線の輪郭度とは、理論的に正確な寸法によって定められた幾何学的に正しい輪郭からの線の輪郭の狂いの大きさをいう。 |
| 面の輪郭度公差 | 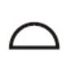 |
面の輪郭度とは、理論的に正確な寸法によって定められた幾何学的輪郭からの面の輪郭の狂いの大きさをいう。 |
| 平行度公差 | 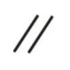 |
平行度とは、データム直線又はデータム平面に対して平行な幾何学的直線又は幾何学的平面からの平行であるべき直線形体又は平面形体の狂いの大きさをいう。 |
| 直角度公差 | 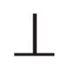 |
直角度とは、データム直線又はデータム平面に対して直角な幾何学的直線又は幾何学的平面からの直角であるべき直線形体又は平面形体の狂いの大きさをいう。 |
| 斜面度公差 |  |
傾斜度とは、データム直線又はデータム平面に対して理論的に正確な角度をもつ幾何学的直線又は幾何学的平面からの理論的に正確な角度をもつべき直線形体又は平面形体の狂いの大きさをいう。 |
| 位置度公差 |  |
位置度とは、データム又は他の形体に関連して定められた理論的に正確な位置からの点、直線形体又は平面形体の狂いの大きさをいう。 |
| 同軸度公差又は同心度公差 |  |
同軸度とは、データム軸直線と同一直線上にあるべき軸線のデータム軸直線からの狂いの大きさをいう。平面図形の場合には、データム円の中心に対する他の円形形体の中心の位置の狂いの大きさを同心度という。 |
| 対称度公差 |  |
対称度とは、データム軸直線又はデータム中心平面に関して互いに対称であるべき形体の対称位置からの狂いの大きさをいう。 |
| 円周振れ公差 |  |
円周振れとは、データム軸直線を軸とする回転面をもつべき対象物又はデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した位置又は任意の位置で指定した方向に変位する大きさをいう。 |
| 全振れ公差 |  |
全振れとは、データム軸直線を軸とする円筒面をもつべき対象物又はデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した方向に変位する大きさをいう。 |
4. 幾何公差の公差域の定義及び図示例とその解釈
平面度公差、平行度公差、円周振れ・全振れ公差について説明します。
1)平面度公差
| 公差域の定義 | 図示例とその解釈 |
|---|---|
公差域は、tだけ離れた2つの平行な平面の間に挟まれた領域です。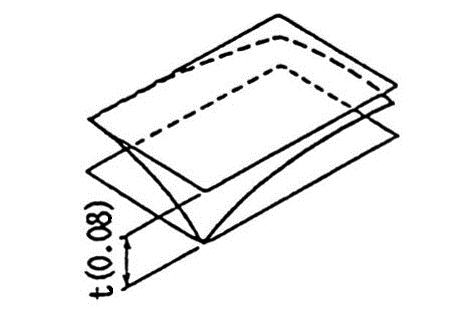 |
この表面は、0.08mmだけ離れた2つの平行な平面の間になければなりません。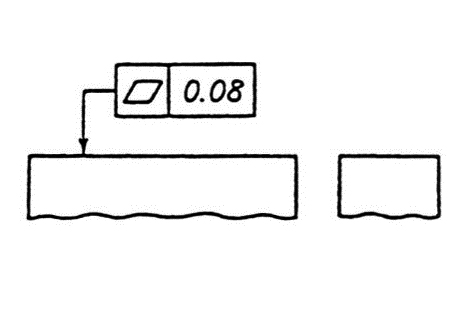 |
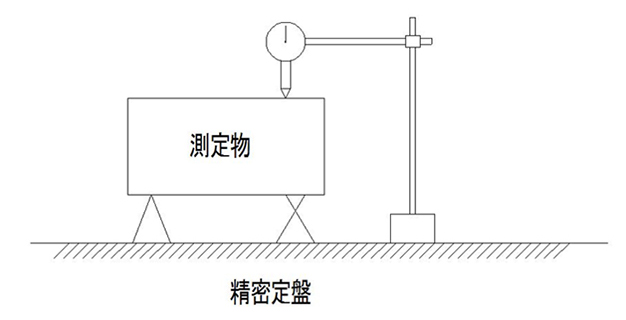
(測定方法例)
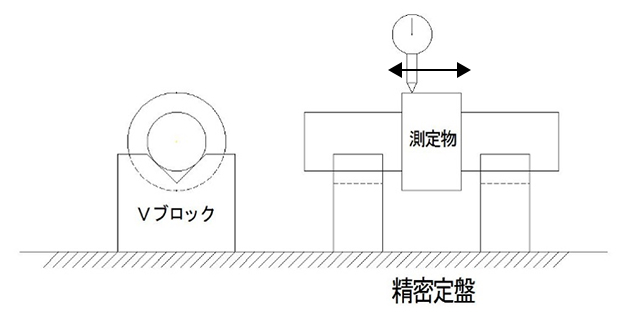
定盤に測定面が平行になるように設定し、さらにダイヤルゲージによって面全体を測定し、その最大最小の差を平面度とします。
2)平行度公差
| 公差域の定義 | 図示例とその解釈 | |
|---|---|---|
| (a) | 公差域は、データム平面に平行で、tだけ離れた2つの平行な平面の間に挟まれた領域である。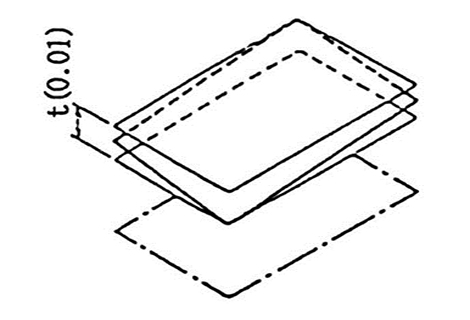 |
指示線で矢の示す軸線は、データム軸直線Aに平行で、かつ、指示線の矢の方向に0.01mmだけ離れた2つの平面の間になければならない。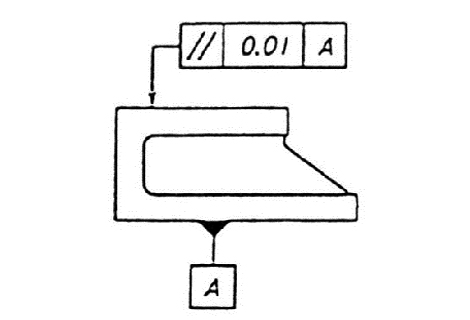 |
| (b) | 指示線の矢で示す面上で、任意に選んだ長さ100mmの上のすべての点は、データム平面Aに平行で、かつ、指示線の矢の方向に0.01mmだけ離れた2つの平面の間になければならない。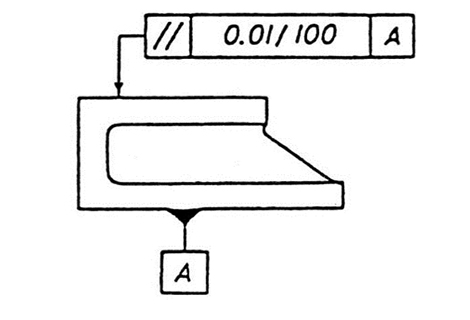 |
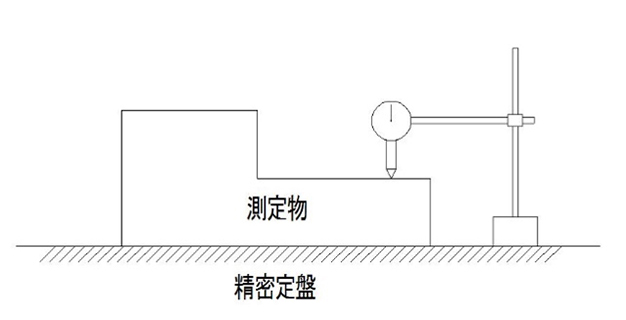
(測定方法例)
データム面を定盤に接地し、ダイヤルゲージによって測定面全体を測定し、その最大最小の差を平行度とします。
3)円周振れ・全振れ公差
| ア)円周振れ公差 | ||
|---|---|---|
| 公差域の定義 | 図示例とその解釈 | |
| 公差域は、データム軸直線に垂直な任意の測定平面上でデータム軸直線と一致する中心をもち、半径方向にtだけ離れた2つの同心円の間の領域である。 振れは一般には、軸線の周りの完全な1回転について適用されるが、1回転のうちの一部分に適用を限定することもできる。 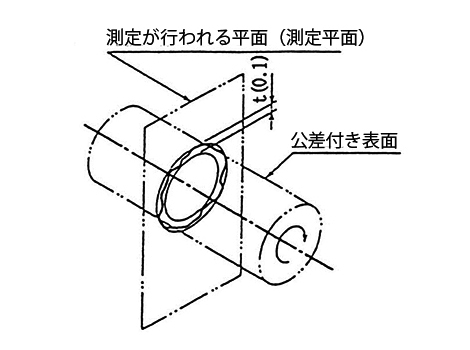 |
指示線で矢の示す円筒面の半径方向の振れは、データム軸直線A-Bに関して1回転させたときに、データム軸直線に垂直な任意の測定平面上で、0.1mmを超えてはならない。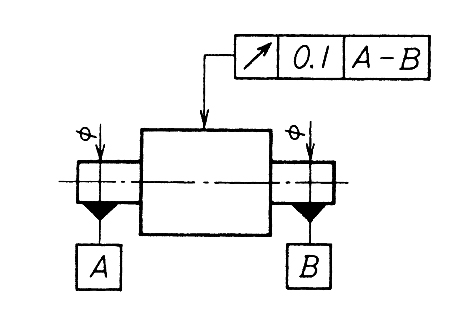 指示線の矢で示す円筒面の一部分 [図(a)では太い一点鎖線で示す範囲、図(b)では扇形の円筒部分]の半径方向の振れは、公差付き形体部分を、データム軸直線Aに関して回転させたときに、データム軸直線に垂直な任意の測定平面上で0.2mmを超えてはならない。 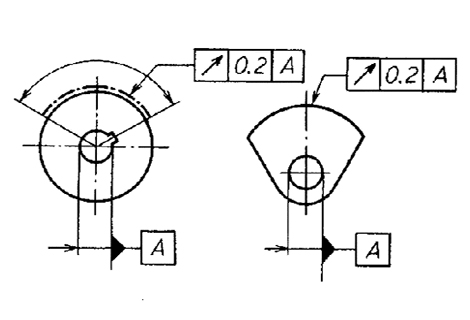 |
|
| イ)全振れ公差 | ||
| (a) | 公差域は、データム軸直線に一致する軸線をもち、半径方向にtだけ離れた2つの同軸円筒の間の領域である。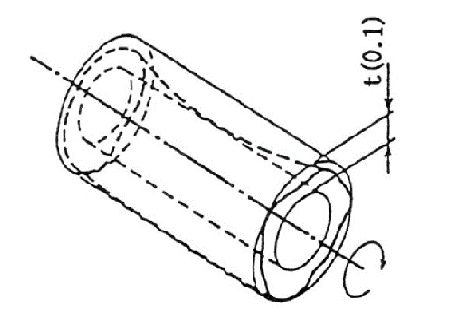 |
指示線の矢で示す面上で、任意に選んだ長さ100mmの上のすべての点は、データム平面Aに平行で、かつ、指示線の矢の方向に0.1mmだけ離れた2つの平面の間になければならない。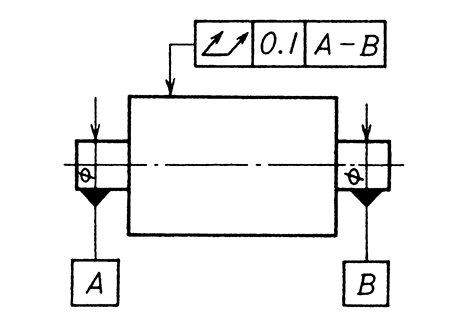 |
| (b) | 公差域は、データム軸直線に垂直で、データム軸直線方向にtだけ離れた2つの平行な平面の間に挟まれた領域である。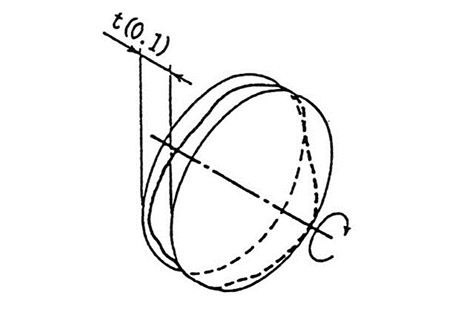 |
指示線の矢で示す円筒側面の軸方向の全振れは、この側面と測定具との間で半径方向に相対移動させながら、データム軸直線Dに関して円筒側面を回転させたときに、円筒側面上の任意の点で0.1mmを超えてはならない。 測定具または対象物の相対移動は、理論的に正確な輪郭線に沿い、データム軸直線に対して正しい位置で行われなければならない。 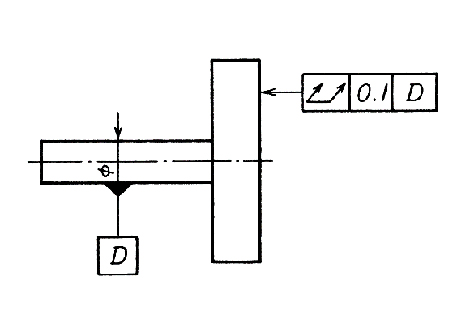 |
(測定方法例)
ア)円周振れ公差
データム軸直線を2つの同一Vブロックによって固定します。測定面にダイヤルゲージをあて、1回転中の読みの最大差を円周振れとします。
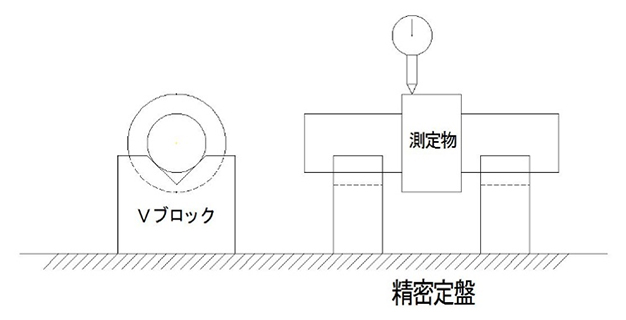
イ)全振れ公差
データム軸直線を2つの同一Vブロックによって固定します。測定面にダイヤルゲージをあて、ダイヤルゲージを移動しながら数回転中の読みの最大差を全振れとします。