第4回 平行曲げの展開長
第4編-2
第4編 展開寸法の求め方
1. 外側寸法加算法
2. 平行曲げの展開長の求め方
前項で解説した外側寸法加算法により、代表的な形状の展開長さを求めてみましょう。
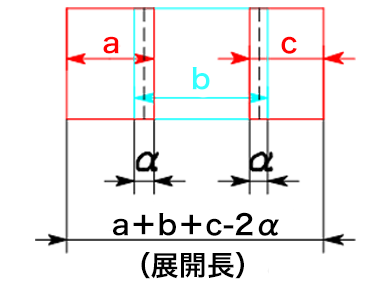
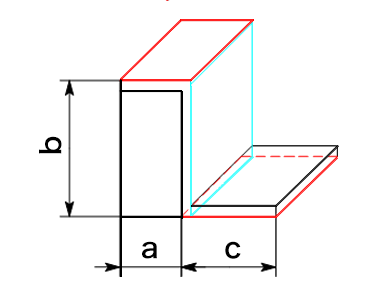
1) コの字曲げ
外側寸法a,b,cを加え、伸び補正値αを曲げ回数分引きます。
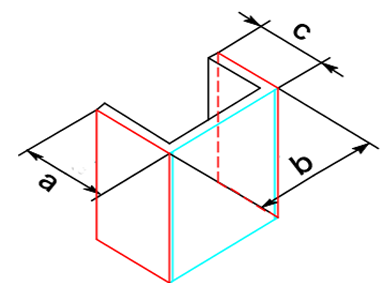
面合成の考え方
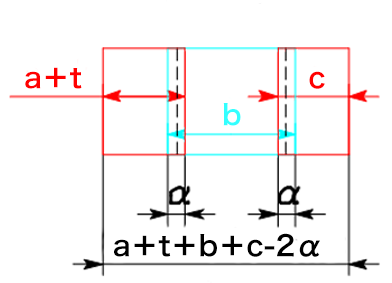
2) Z曲げ
aは内側寸法なので、板厚tを加えて外側寸法にします。
面合成の考え方
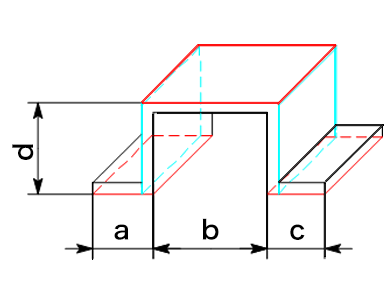
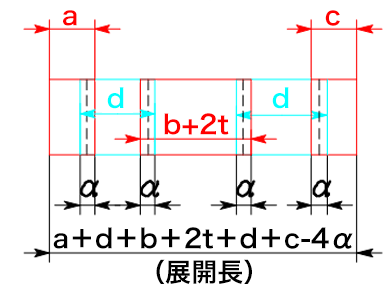
3) ハット曲げ
bは内側寸法なので、両側の板厚を加えて外側寸法にします。dは2回加えます。
面合成の考え方
4) 切り欠き寸法の求め方 – 1
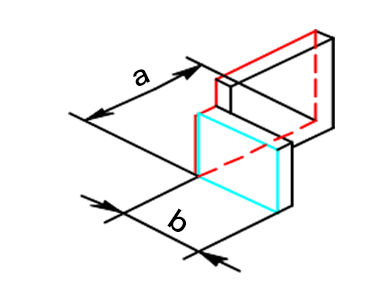
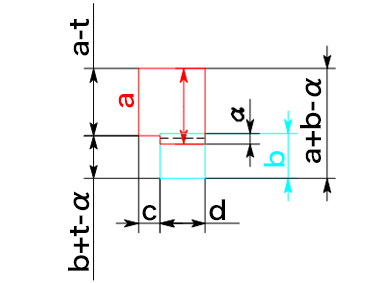
切り欠きの位置が底面より板厚分上になる曲げ形状です。
縦方向の全体の長さa+b-αから、切り欠きの上の長さa-tを引くと切り欠きの縦の長さb+t-αが求められます。
面合成の考え方
第三角法
展開図
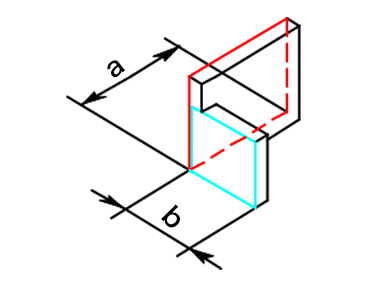
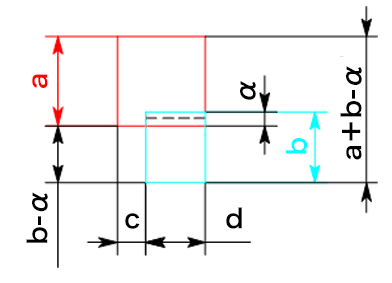
5) 切り欠き寸法の求め方 – 2
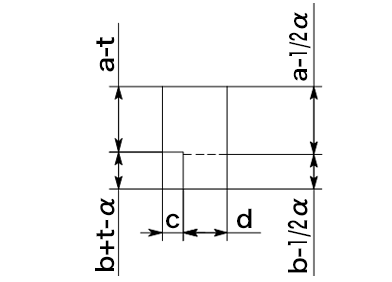
切り欠きの位置が底面と同じ高さになる曲げ形状です。
縦方向の全体の長さa+b-αから切り欠きの上の長さaを引くと、切り欠きの縦の長さb-αが求められます。
面合成の考え方
第三角法
展開図
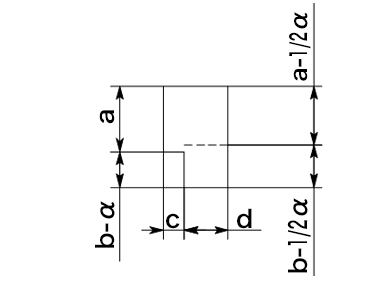
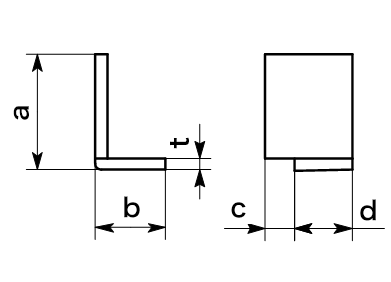
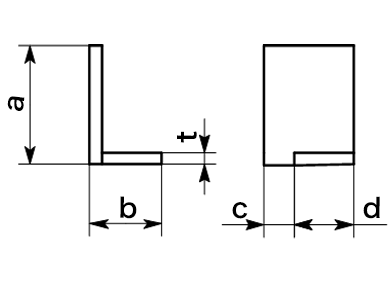
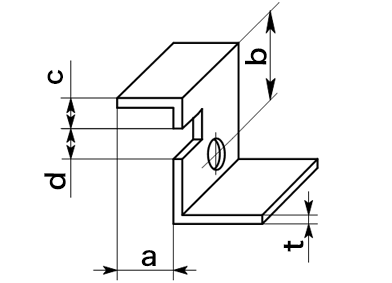
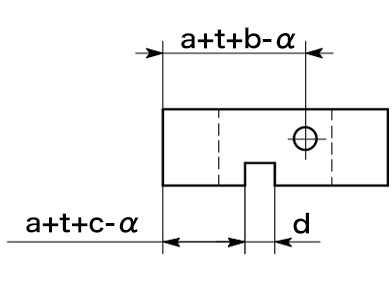
6) 穴、スリットがある場合
aは内側寸法、L形断面の展開計算。
展開図
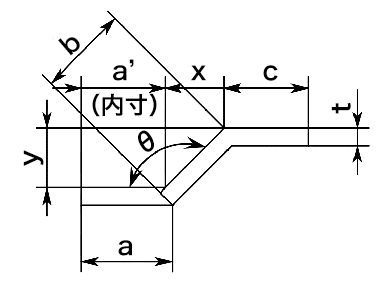
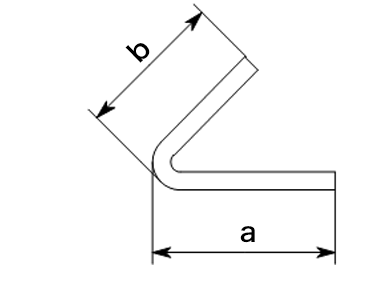
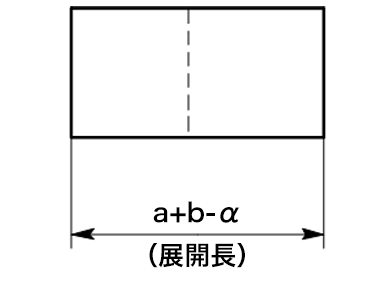
7) 鋭角曲げ
外Rからの寸法を外寸とするのが一般的な計算です。
展開図
外Rからの寸法を外寸とするのが一般的な計算です。
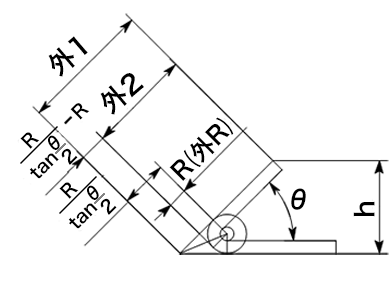
・外1から外2へ変換する場合
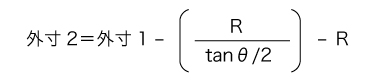
・hから外2へ変換する場合
8) 鈍角曲げ
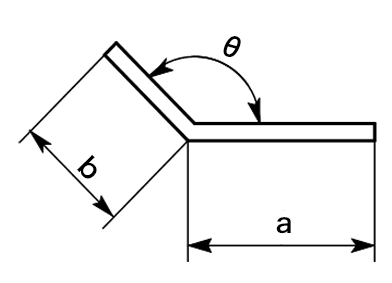
展開図
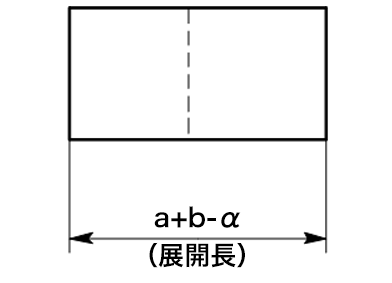
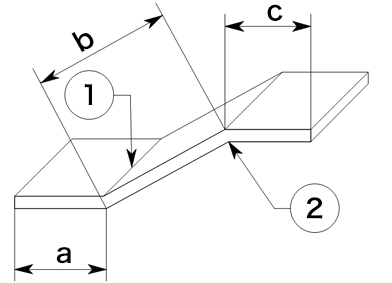
9) 鈍角曲げ(折り返し曲げ)
展開図
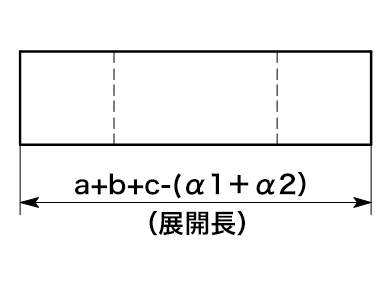
α1は①の伸び補正値
α2は②の伸び補正値
外寸a,bの求め方と展開長の計算式