第5回 箱物の展開長
第4編-3
第4編 展開寸法の求め方
1. 外側寸法加算法
3. 箱物の展開長の求め方
平行曲げだけの時は突き合わせはありませんが、箱物曲げの場合は突き合わせが出てきます。
実務で出てくる突き合わせの形状はパターン化されていますので、ここでは、よく出てくるものについて紹介します。
1) BOX形状(両引きの突き合わせ)
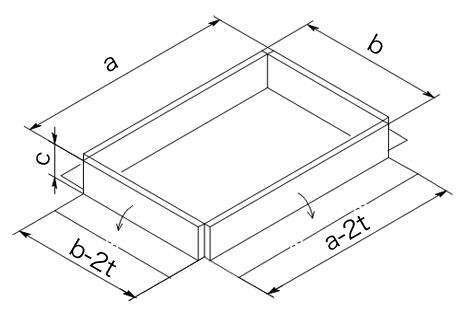
三角法
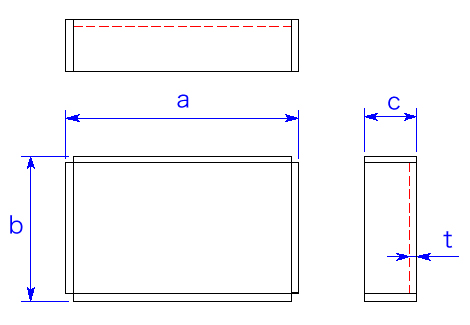
展開図
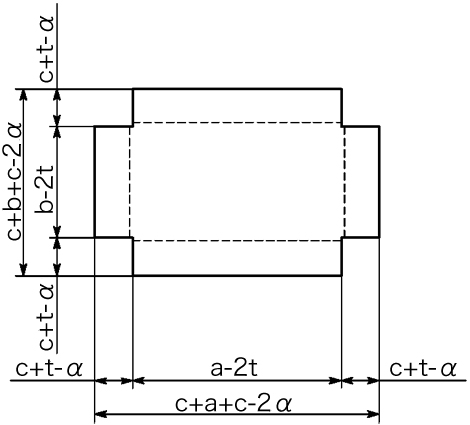
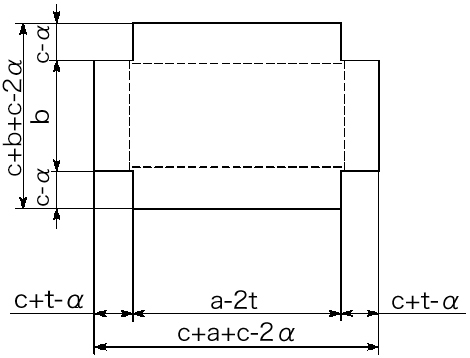
2) BOX形状(片引きの突き合わせ)

三角法
展開図
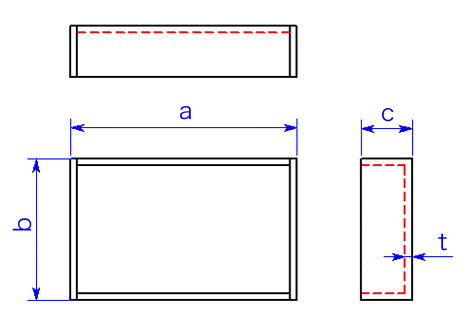
練習問題 3
先に求めたBOX-1展開形状の寸法を計算し、展開図を仕上げましょう!
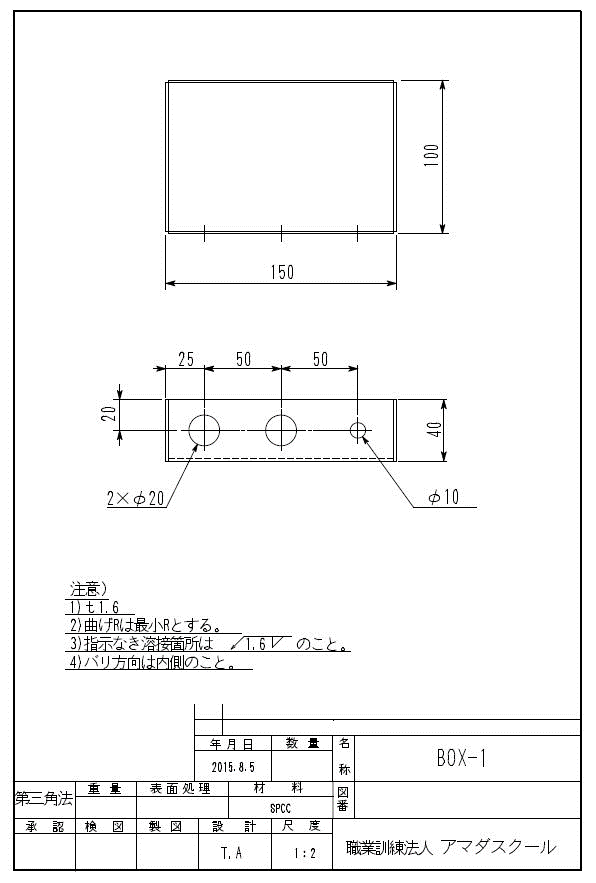
練習問題 3の答えと解説
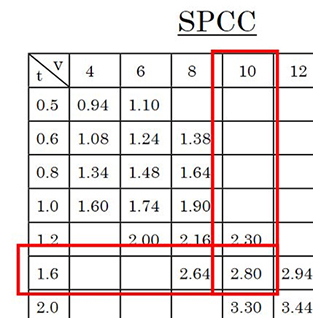
まずは伸び値の確認をします。
材質:SPCC、板厚:1.6mmから
V=6t(第3回参照)より
V=6t=6×1.6=9.6
大きめのV幅:10を選択します。
t=1.6とV=10の交差する値より
伸び値:2.80 となります。
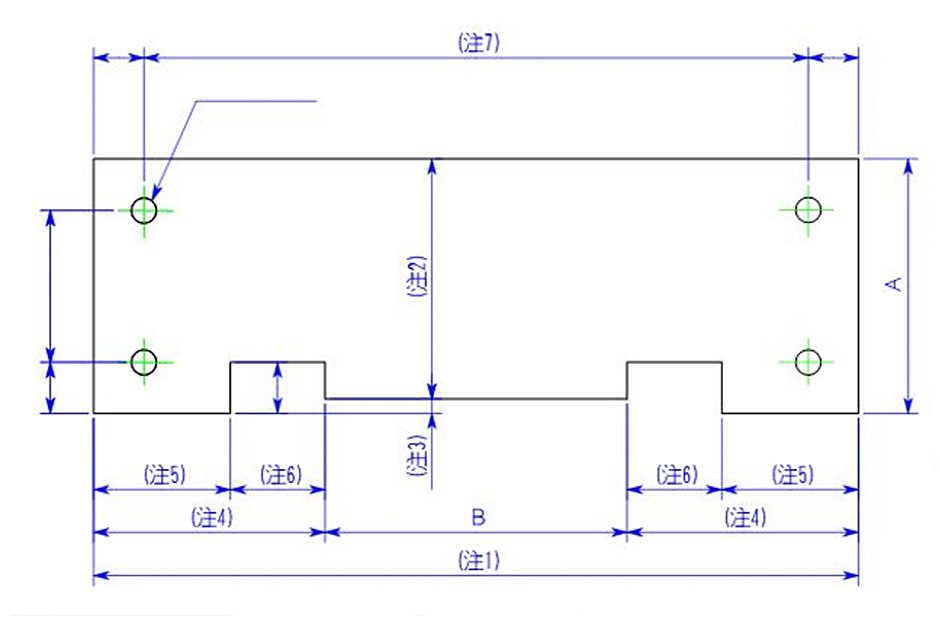
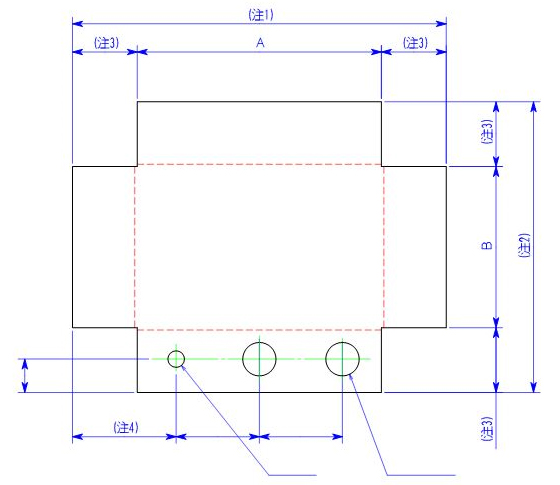
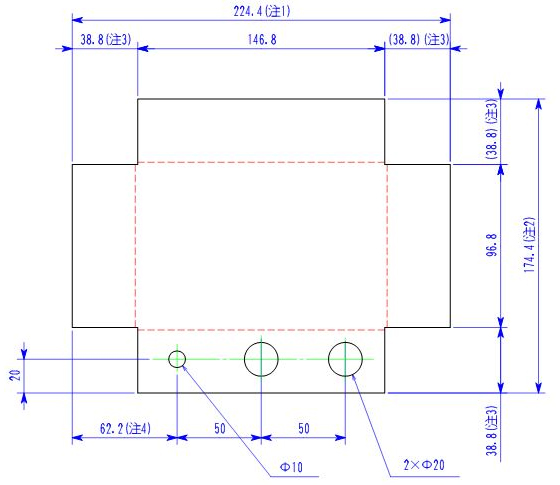
展開寸法計算においては第2編の展開図作成の流れでも説明したように、外形寸法(注1、2)より求めていきます。
注1の求め方
展開長は右の図の太線より求められます。
曲げが2カ所あるのがわかります。
よって、
40+150+40-2×2.8=224.4
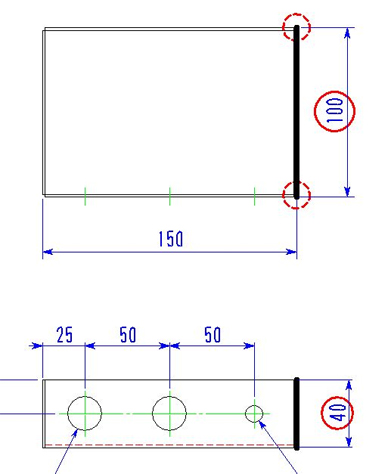
注2の求め方
展開長は左図の太線より求められます。
40mmのフランジが破線部に2カ所あり、曲げが2カ所あるのがわかります。
よって、
40+100+40-2×2.8=174.4
次にA、Bの寸法を記入します。
A=150-2×1.6=146.8
B=100-2×1.6=96.8
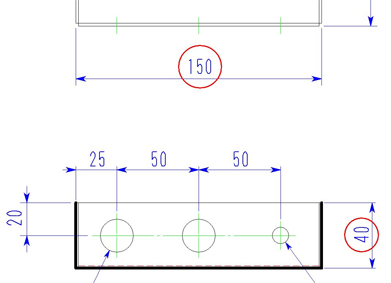
次に切り欠き寸法(注3)、穴までの寸法(注4)を求めます。
注3の求め方
展開長は左図の太線より求められます。
突き合わせ部が板厚分出ているのがわかります。
よって、
40+1.6-2.8=38.8
もしくは今回、左右対称形なので、注2からBを引き、2で割ります。
(174.4-96.8)÷2=38.8
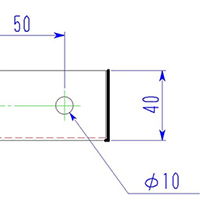
注4の求め方
展開長は左図の太線より求められます。
曲げ部が1カ所あるのがわかります。
よって、
40+(150-25-50-50)-2.8=62.2
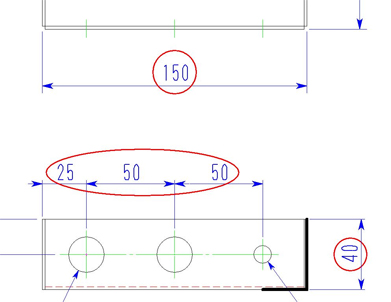
展開図
演習問題 3
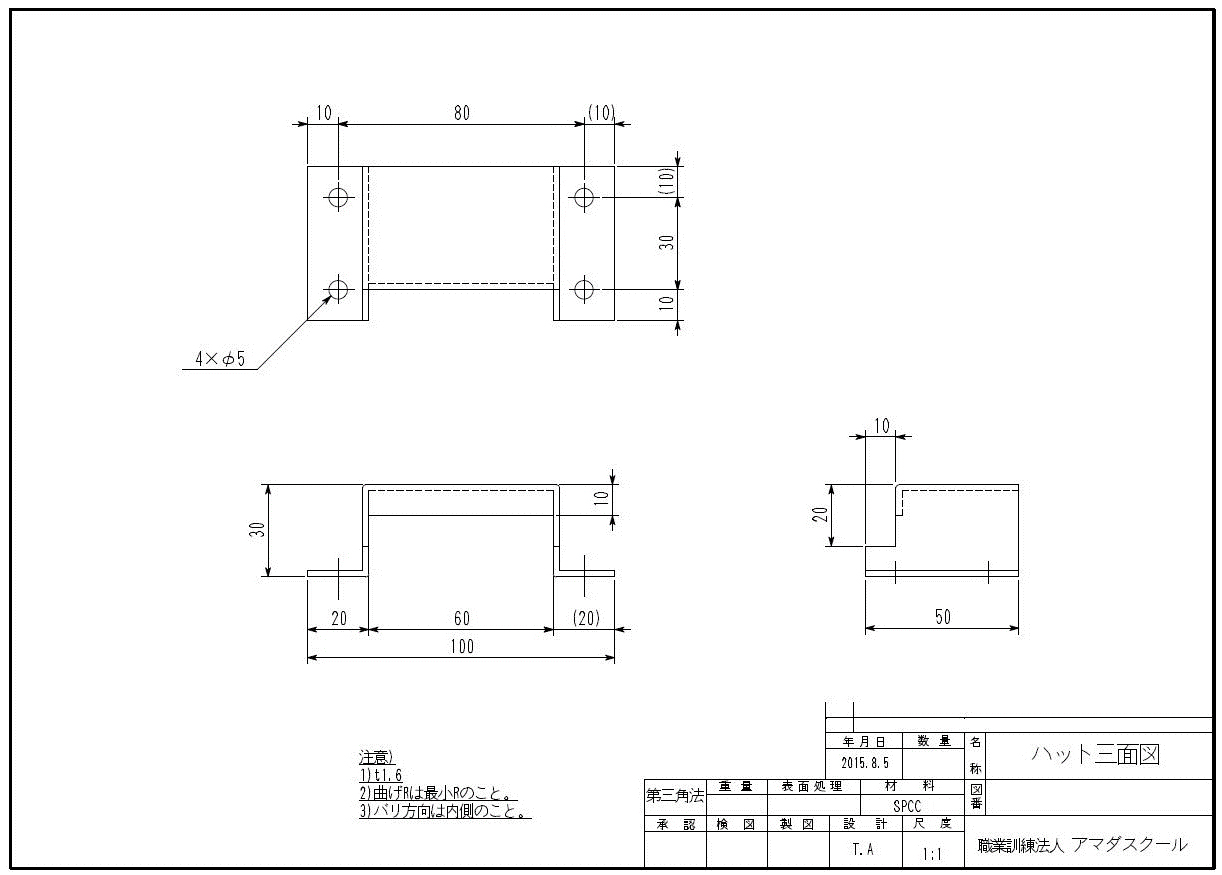
「ハット三面図」の展開計算を行いましょう!