第8回 曲げ線寸法の練習
第4編-6
今回は前回の講座を踏まえた練習問題の回となります。
前回の講座を振り返り、練習問題を解いてみましょう。
練習問題 4
下記の「V字切欠」でVノッチ形状の展開を行いましょう!
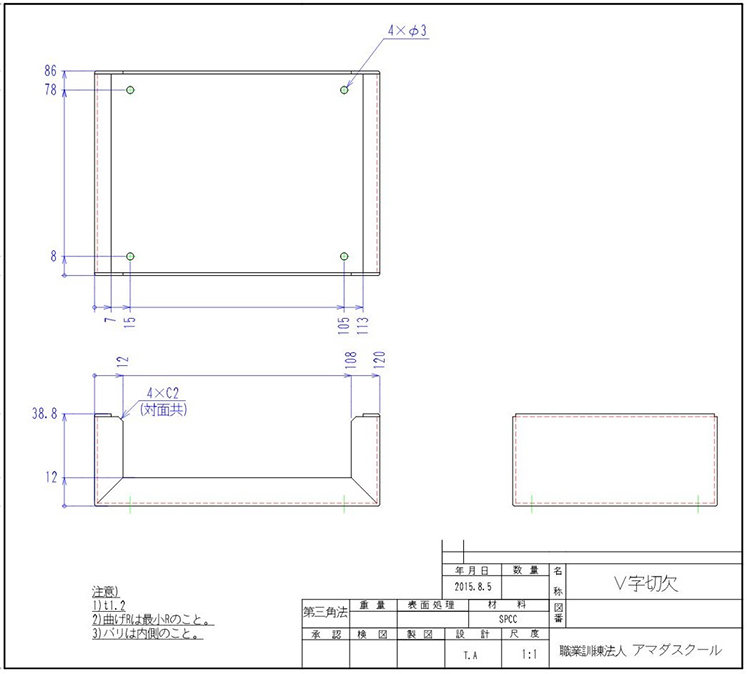
- Q1. 材質、板厚は?
- Q2. 面は何面ありますか?
- Q3. 各面の形状を描いてください
- Q4. 展開形状を描いてください
- Q5. 展開寸法を計算し、展開寸法を書いてください
- Q6. Vノッチ90°曲げの計算式を用いて曲げ線寸法を書いてください
練習問題 4の答えと解説
Q1. 材質、板厚は?
答え:SPCC 1.2mm
☆この図面では表題欄に材質が、注記欄に板厚が記載されています。
Q2. 面は何面ありますか?
答え:11面
- ・オレンジ色の平面図:①、②、③の3面
- ・ミドリ色の正面図:⑥、⑧、⑩の3面と反対側に対となる⑦、⑨、⑪の3面
- ・水色の側面図:④と反対側に対となる⑤の2面
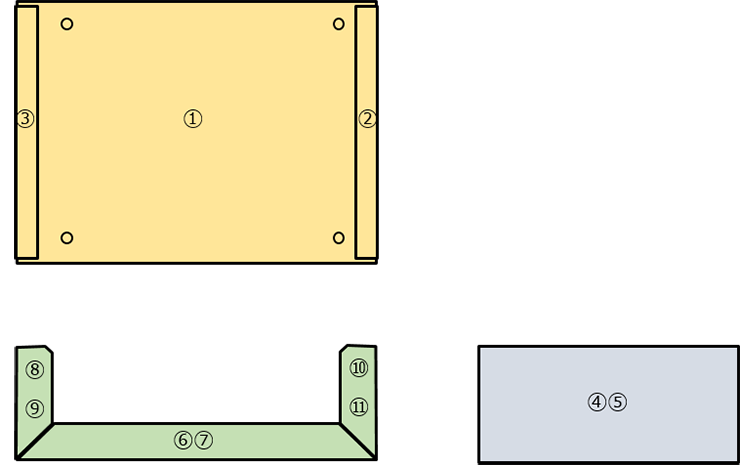
Q3. 各面の形状を描いてください
答え:下図参照
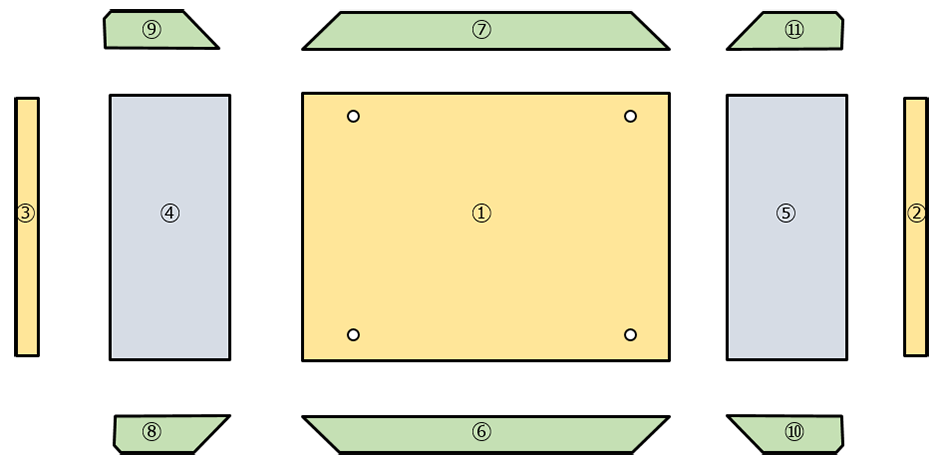
Q4. 展開形状を描いてください
答え:各面を曲げ部で接合し、曲げ線を貼線に変更すると下図のように展開形状となります
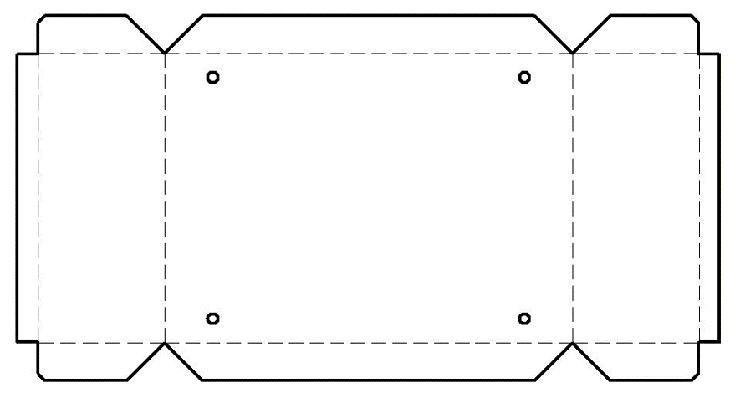
Q5. 展開寸法を計算し、展開寸法を書いてください
Q6. Vノッチ90°曲げの計算式を用いて曲げ線寸法を書いてください
答え:下図参照
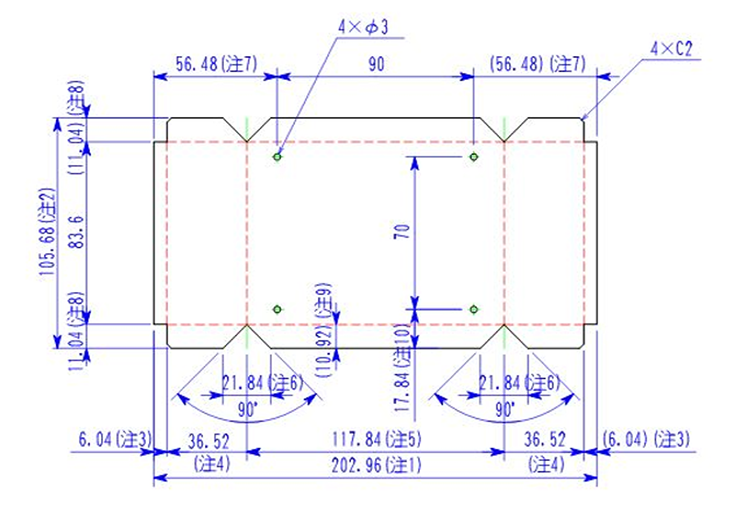
解説:展開寸法の計算
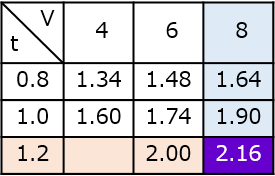
まず、伸び値の確認をします。※第3回参照
SPCC 1.2mm の材料なのでV幅8mmを選択
t=1.2とV=8の交差する2.16が伸び値となります。
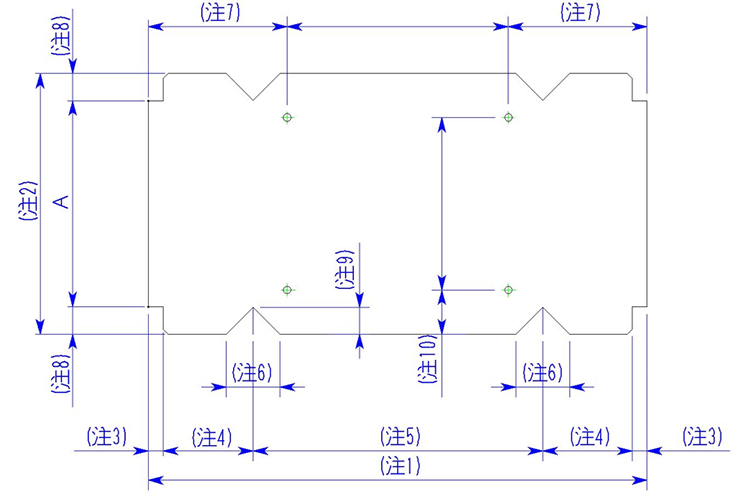
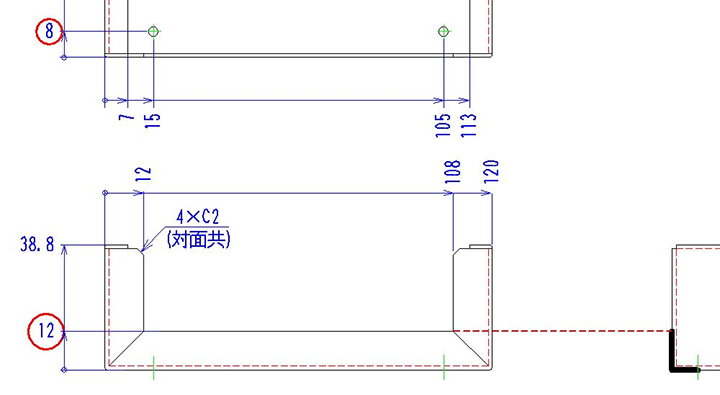
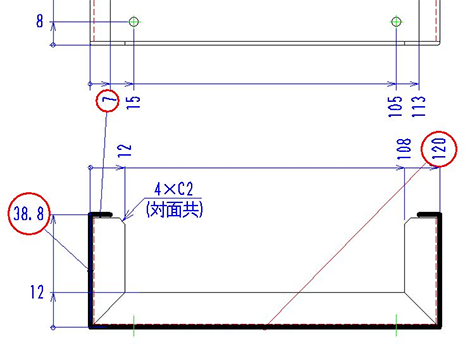
注1 の展開長計算
展開長は右図の太線より求められます。
曲げが4箇所あるのがわかります。
よって、
7+38.8+120+38.8+7-4×2.16=202.96
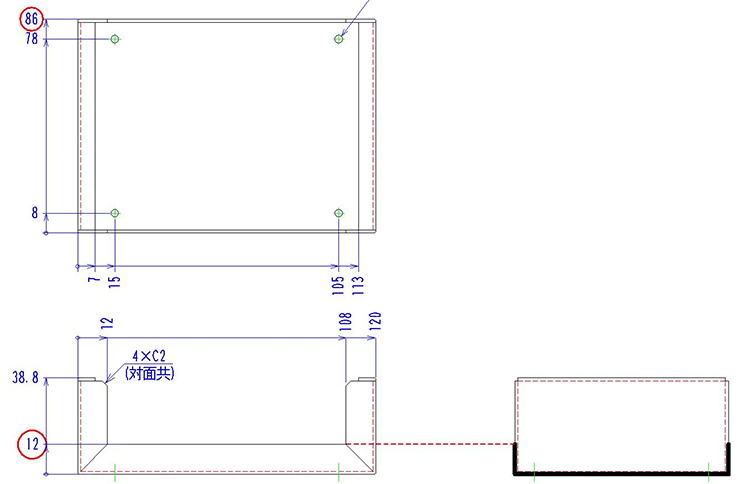
注2 の展開長計算
展開長は右図の太線より求められます。
曲げが2箇所あるのがわかります。
よって、
12+86+12-2×2.16=105.68
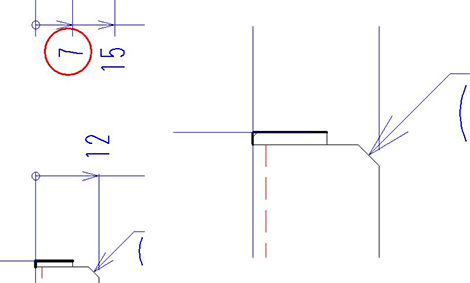
注3 の展開長計算
展開長は右図の太線より求められます。
突合せ部が出ているのがわかります。
よって、
7+1.2-2.16=6.04
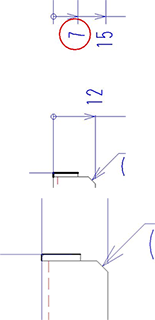
注4 の展開長計算
展開長は右図の太線より求められます。
片側が曲げ線までの寸法になるのがわかります。
よって、
38.8-1.2-(2.16/2)=36.52
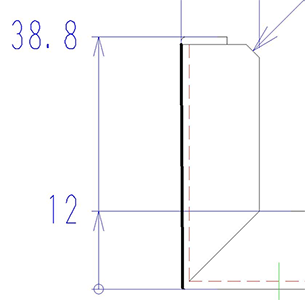
注5 の展開長計算
展開長は右図の太線より求められます。
両側が曲げ線までの寸法になるのがわかります。
よって、
120-2×(2.16/2)=117.84

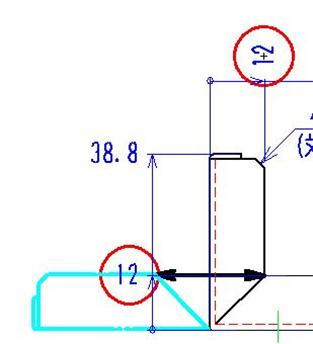
注6 の展開長計算
展開長は右図の太矢印線より求められます。
中心に曲げがあるのがわかります。
よって、
12+12-2.16=21.84
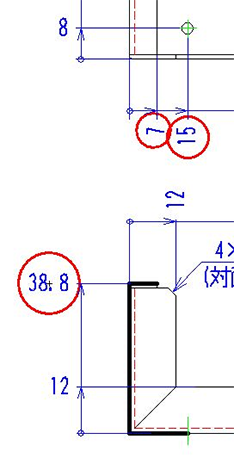
注7 の展開長計算
展開長は右図の太線より求められます。
曲げが2箇所あるのがわかります。
よって、
7+38.8+15-2×2.16=56.48
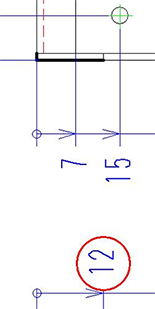
注8 の展開長計算
展開長は右図の太矢印線より求められます。
突合せ部が出ているのがわかります。
よって、
12+1.2-2.16=11.04
注9 の展開長計算
展開長は右図の太線より求められます。
片側が曲げ線までの寸法になるのがわかります。
よって、
12-(2.16/2)=10.92
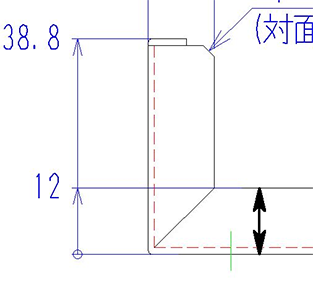
注10 の展開長計算
展開長は右図の太線より求められます。
曲げが1箇所あるのがわかります。
よって、
12+8-2.16=17.84