第11回 内側寸法加算法、
中立面基準法
第4編-9
第4編 展開寸法の求め方
2. 内側寸法加算法
内側寸法加算法の計算方法は、外側寸法加算法と考え方は同じで、外側寸法加算法では外寸で展開長を計算するのに対して、内側寸法加算法は内寸で計算する方法です。
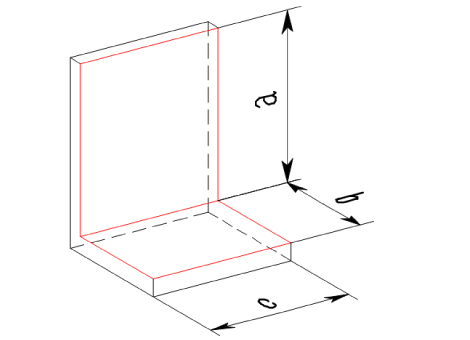
立体図
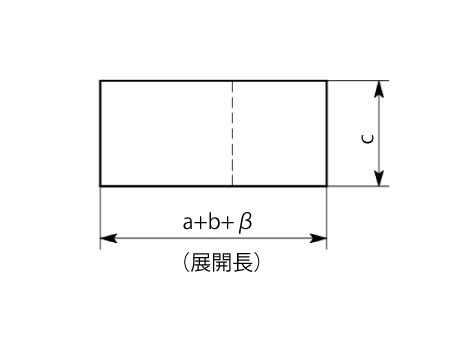
展開図
展開長=a+b+β
a,b,c,は板の内側の寸法で内寸といいます。(赤線部分)
βはちぢみ補正値(内伸び補正値)といい、曲げ加工前の展開長と、加工後の内側寸法(a+b)の差を計算することにより求めることができます。
βは外側寸法加算法と同じく、各工場において実際に加工してデータを持っているのが一般的です。
βは外側寸法加算法の伸び補正値(α)と次式の関係があるので参考にしてください。
90°曲げの時
β=2tーα
鈍角曲げの時
β=2t+tan 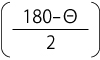 ーα
ーα
(Θ=90°の時 β=2t-α)
3. 中立面基準法
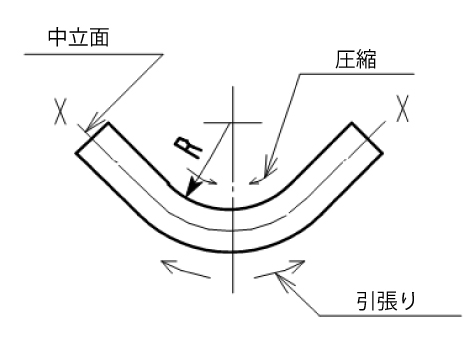
パンチとダイによって材料に変形を与え、V字形に加工し終わった場合を考えてみると、材料の内側(パンチ側)は圧縮ひずみ、外側(ダイ側)は引っ張りひずみが生じています。
そのひずみの大きさは、板の表面部が最も大きくて順次板の内部に向かって小さくなっていき、中心部近くにおいては、圧縮ひずみや引っ張りひずみもない面が想像されます。
このような面を中立面(立体的に考えた場合は面、板の断面で考えた場合は線)と称し下図のX-X線で表わされ、この長さを求めて展開寸法を出す方法が中立面基準法です。
この方法は机上の計算であり、近似値です。精度の高い製品が要求される時は、外側寸法加算法で計算する必要があります。
1. 中立面基準法ー1(曲げ R≧5tの場合)
曲げ半径が板厚の5倍または、5倍以上になると曲げた個所の板厚の変化はなく、伸びもほとんどありません。すなわち中立面は、板厚tの中心線上にあると考えて差し支えない場合の計算方法と言えます。
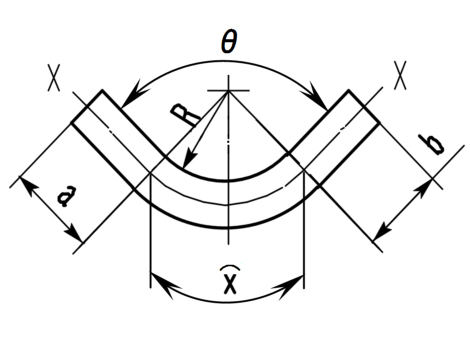
上図において展開長をLとすると、次式のようになります。
L=a+x+b x=〔(180ーΘ)/360〕・2π (R+t/2)
ここで、θ=90°の時はL=a+1.57 (R+t/2) +bとなります。
2. 中立面基準法ー2(曲げR<5tの場合)
板厚に比べて曲げ半径が小さい時は、下図のように素板が伸ばされて薄くなり、中立面は内側へと寄っていきます。
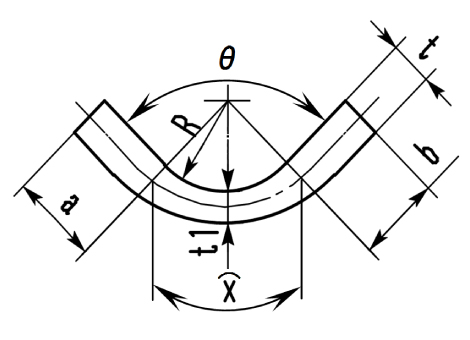
板厚の減少率(t1/t)は(R/t)の値の大きさによって下表のようにグループ化されています。
| グループ | R/t | t1/t |
|---|---|---|
| A | 0.5未満 | 約0.4 |
| B | 0.5~1.5 | 0.6 |
| C | 1.5~3.0 | 0.66 |
| D | 3.0~5.0 | 0.8 |
| E | 5.0~ | 1.0 |
上表から解るようにAグループ(R/tが0.5未満)の場合には、曲げ終わったあとの板厚t1は元の板厚の40%になってしまいます。
Eグループ(R/tが1~)の場合は、板厚の変化はありません。
例えば、板厚1.2mmに対して1.5mmの曲げ半径で加工すると仮定した場合、R/tは1.25となってBグループに入りt1/tは0.6となります。
すなわち、曲げ加工の結果、1.2mmの素板は1.2×0.6=0.72mmまで薄くなってしまうため、中立面は内側面より0.36mmのところまで寄ってきているということになります。
この中立面の長さが展開長となるので計算式は次のようになります。
L=a+x+b x=〔(180ーΘ)/360〕・2π (R+t1×1/2)
ここで、Θ=90°の時はL=a+1.57 (R+t1×1/2) +bとなります。
演習問題 8
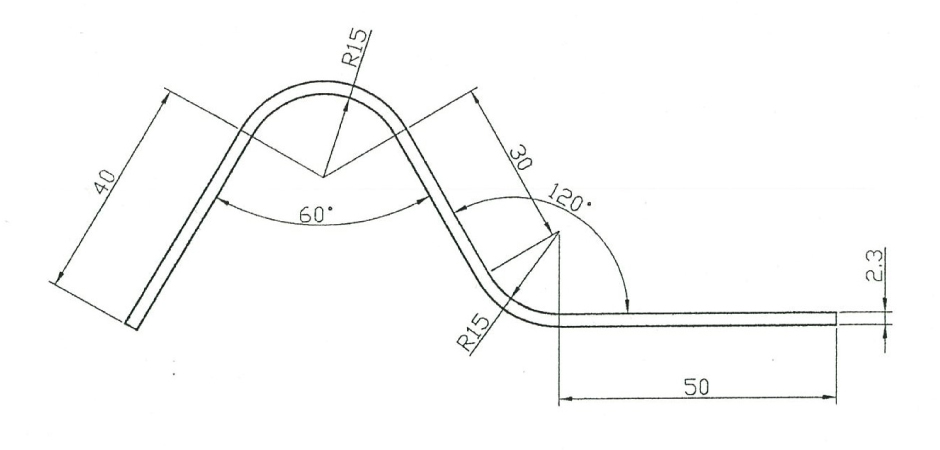
図示の展開長さを求めましょう!
中立面基準法(R≧5t)の演習問題です。
1. 中立面基準法ー1を参考に解いてみましょう!
ただし、円周率πは3.14とします